All vectors of the form (a, b, c), where b = a +c+ 1. b. If \(W = \mathrm{span} \left\{ \vec{v}_1, \cdots, \vec{v}_n \right\}\) then \(W\) is a subspace of \(V\). As well, this calculator tells about the subsets with the Call it \(k\). It is important to note that a basis for a vector space is not unique. Let \(V\) be a vector space with \(W \subseteq V\). compare electrolytes in sports drinks science project. Let \(V\) be the vector space of polynomials of degree no more than 3, denoted earlier as \(\mathbb{P}_{3}\). Web). of the vectors
Remember the de nition of dimension is the size of a basis.) However, an onlineDeterminant Calculator allows you to calculate the determinant of the given matrix input elements. Why is it forbidden to open hands with fewer than 8 high card points? Let \(W \subseteq \mathbb{P}_2\) be all polynomials of degree two or less which have \(1\) as a root. Let \(A=\left [\begin{array}{rr} a & b \\ c & d \end{array}\right ] \in\mathbb{M}_{22}\). is called
The proper subset is a special subset. 
These you have to answer. When determining spanning sets the following theorem proves useful. Let \(V\) be a vector space. See details Help for whatever math you're studying Pre Algebra Fraction Linear equations 1 Arithmetic Negative numbers Are the operations of \(V\) defined on \(W?\) That is, when you add vectors of \(W\) do you get a vector in \(W?\) When you multiply a vector in \(W\) by a scalar, do you get a vector in \(W?\) Yes. + 1 Amzoti Apr 18, 2013 at 1:01 Add a comment 
Then by Lemma 9.3.2, we could find a fourth polynomial in \(\mathbb{P}_2\) to create a new linearly independent set containing four polynomials. Hence this is a basis for \(\mathbb{P}_2\). Continuing this way, the process must stop before \(n+1\) steps because if not, it would be possible to obtain \(n+1\) linearly independent vectors contrary to the exchange theorem, Theorem \(\PageIndex{3}\). Hence \(T\) is a basis. Then since \(r>s,\) it follows that \(l\leq s Mathforyou 2023
If there had been only three pivot columns in this matrix, then we would not have had a basis for \(V\) but we would at least have obtained a linearly independent subset of the original set of vectors in this way. It is obvious that all the algebraic laws hold on \(W\) because it is a subset of \(V\) and they hold on \(V\). . As well, this calculator tells about the subsets with the specific number of elements. The reduced row echelon form of the matrix: To find the null space, solve the matrix equation: [1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1] [x_1x_2x_3x_4] = [0 0 0 0]. The null space vector Y can be used to identify these linear relationships. Suppose \(n > m.\) Then since the vectors \(\left\{ \vec{u} _{1},\cdots ,\vec{u}_{m}\right\}\) span \(V,\) there exist scalars \(c_{ij}\) such that \[\sum_{i=1}^{m}c_{ij}\vec{u}_{i}=\vec{v}_{j}.\nonumber \] Therefore, \[\sum_{j=1}^{n}d_{j}\vec{v}_{j}=\vec{0} \text{ if and only if }\sum_{j=1}^{n}\sum_{i=1}^{m}c_{ij}d_{j}\vec{u}_{i}= \vec{0}\nonumber \] if and only if \[\sum_{i=1}^{m}\left( \sum_{j=1}^{n}c_{ij}d_{j}\right) \vec{u}_{i}=\vec{ 0}\nonumber \] Now since \(\{\vec{u}_{1},\cdots ,\vec{u}_{n}\}\) is independent, this happens if and only if \[\sum_{j=1}^{n}c_{ij}d_{j}=0,\;i=1,2,\cdots ,m.\nonumber \] However, this is a system of \(m\) equations in \(n\) variables, \(d_{1},\cdots ,d_{n}\) and \(m This is a cumbersome task, and therefore a shorter procedure is used to verify a subspace. It will then follow that \(U=W\). Why would I want to hit myself with a Face Flask? The best answers are voted up and rise to the top, Not the answer you're looking for?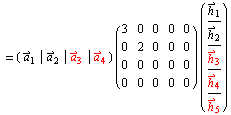 
Clearly a solution exists for all \(a,b,c\) and so \(S\) is a spanning set for \(\mathbb{P}_2\). Now suppose that the dimension of \(W\) is \(n\). A subspace is just a vector space 'contained' in another vector space. Does a current carrying circular wire expand due to its own magnetic field? Using an RC delay circuit on an NPN BJT base, Replacing one feature's geometry with another in ArcGIS Pro when all fields are different, Uniformly Lebesgue differentiable functions, Seal on forehead according to Revelation 9:4. barbecue festival 2022; olivia clare friedman net worth. { then 1) It is a subset of \( \mathbb{R}^3 = \{ (x,y,z) \} \) 3 These are: The key property here is that the original matrix and its reduced row echelon form have the same null and rank. Download Wolfram Notebook. 
Here well explain subset vs proper subset difference and how to find subsets of a given set. Then \(W\) has a basis with no more than \(n\) vectors. Write the vector v = (2, 2, 2) as the sum of a vector in S and a vector orthogonal to S. The cardinality of the empty set is 0 because the empty set does not contain any elements. \[\begin{array}{ccc} a+b & = & a + c \\ -b & = & b + d \\ c + d & = & -c \\ -d & = & -d \end{array}\nonumber\], \[\begin{array}{rcc} b - c & = & 0 \\ -2b - d & = & 0 \\ 2c + d & = & 0 \end{array}.\nonumber \]. These are: The key property here is that the original matrix and its reduced row echelon form have the same null and rank. It follows that \(p(1) = 0\) and \(q(1) = 0\). by remote non clinical physician assistant jobs. WebAdvanced Math questions and answers In Exercises 1-2, use the Subspace Test to determine which of the sets are subspaces of R. 1. a. So $A+B\in U_1$. Webinterior angle sum regular million-gon. Use this online subset calculator which fined the subsets containing the number of elements. The number of linear relationships between attributes is given by the size of the null space. so $(x_1+x_2,y_1+y_2,z_1+z_2) = (x_1,y_1,z_1) + (x_2,y_2,z_2) \in S$. Note that removing any one of \(1, x^2\), or \(x^2 + 1\) will result in a basis. If \(W\) is not equal to \(V\), then let \(\vec{v}\) be a vector of \(V\) which is not contained in \(W.\) Thus \(\vec{v}\) is not in \(\mathrm{span}\left\{ \vec{w}_{1},\cdots ,\vec{w} _{n}\right\}\) and by Lemma 9.7.2, \(\left\{ \vec{w}_{1},\cdots ,\vec{w}_{n},\vec{v}\right\}\) is linearly independent which contradicts Theorem \(\PageIndex{3}\) because it would be an independent set of \(n+1\) vectors even though each of these vectors is in a spanning set of \(n\) vectors, a basis of \(V\). WebSPECIFY THE NUMBER OF VECTORS AND THE VECTOR SPACES Please select the appropriate values from the popup menus, then click on the "Submit" button. Does disabling TLS server certificate verification (E.g. \(\mathrm{span}\left\{ \vec{v}_{1},\cdots ,\vec{v}_{n}\right\} = V\), \(\{\vec{v}_{1},\cdots ,\vec{v}_{n}\}\) is linearly independent. Suppose first that \(W\) is a subspace. WebFind an orthonormal basis for the subspace of Euclidean 3 space below. 
The following example will show that two spans, described differently, can in fact be equal. Comments and suggestions encouraged at [email protected]. From the source of Lumen Learning: Using Matrices to Solve Systems of Equations, Matrix Equations, Writing a System of Equations with Matrices, Matrices and Row Operations, Elementary Row Operations (ERO), Produce Equivalent Matrices Using Elementary Row Operations. As you can see, we can verify the two points easily in a general case. WebFind a basis for the subspace of spanned by the following vectors. Let \(V\) be a vector space. such as at least one of then is not equal to zero (for example
Figure 2 Example 1: Let S be the 2dimensional subspace of R 3 spanned by the orthogonal vectors v 1 = (1, 2, 1) and v 2 = (1, 1, 1). Feel hassle-free to account this widget as it is 100% free, simple to use, and you can add it on multiple online platforms. our expert tutors can assist you with everything from homework to test prep. Why should reason be used some times but not others? Thus \(m\in S\). It must stop since otherwise, you could obtain a linearly independent set of vectors having more than \(n\) vectors which is impossible. Similarly it cannot happen that \(m > n\). | 0 y y y To show that W V is a subspace, we have to show that it satisfies the vector Suppose \(c_{k}\neq 0.\) Then solve for the vector \(\vec{v}_{k}\) in terms of the other vectors. It only takes a minute to sign up. The number of proper subsets of a given sub-set is \(2^n-1\). WebIs a subspace. (Try to think of an example, and nd a basis for it. The first step matrix null space calculator uses the Gauss Jordan elimination to take the first cell of the first row, x (until it is zero), and remove the following items through atomic row operations. = \left [\begin{array}{rr} 1 & 1 \\ 0 & -1 \end{array}\right ] A \right\}\). The resulting set would be \(\left\{ 1, x^2, x^2 + 1 \right\}\). Any subspace of a vector space \(V\) which is not equal to \(V\) or \(\left\{ \vec{0} \right\}\) is called a proper subspace. WebA basis for a subspace S of Rn is a set of vectors in S that is linearly independent and is maximal with this property (that is, adding any other vector in S to 530 Math Specialists. Knowing the number of subsets and elements is such a time-consuming task but thanks to the free subsets calculator that provides the number of elements in every subset. A basis for \(V\) is \(\left\{ 1,x,x^{2},x^{3}\right\}\). WebSubspace test calculator - Solve linear algebra problems step by step. Then \(V\) is a subspace of itself. The two subspaces described above are called improper subspaces. Let \(\vec{w}_1\) be in \(\left\{ \vec{0} \right\}\) and let \(a\) be an arbitrary scalar. Otherwise, there exists \(\vec{v} _{2}\in V\) which is not in \(\mathrm{span}\left\{ \vec{v}_{1}\right\} .\) By Lemma 9.3.2 \(\left\{ \vec{v}_{1},\vec{v}_{2}\right\}\) is a linearly independent set of vectors. Everybody needs a calculator at some point, get the ease of calculating anything from the source of calculator-online.net. is called
You have the desired basis. Why can I not self-reflect on my own writing critically? I'm currently studying Subspace tests in my linear Algebra module at uni, but am struggling to understand it, can anyone explain how to conduct a SubSpace test? Thus \[\left [ \begin{array}{c} 1 \\ 1 \\ 2 \\ 0 \end{array} \right ]\nonumber \] corresponds to \(2x^{2}+x+1\) through the use of this isomorphism. By Theorem \(\PageIndex{6}\), some subset of \(S\) is a basis for \(\mathbb{P}_2\). Let V be a vector space, and let U and W be subspaces of V. Then. Does every vector in \(W\) have an additive inverse?
I understand the basics of the test in that I need to prove that the subspace is non-empty, and is closed under vector addition and scalar multiplication - but I don't understand how to apply this. Homework Support Online Learning math can be fun and rewarding! By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. \[\begin{aligned} &2x^{2}+x+1,x^{3}+4x^{2}+2x+2,2x^{3}+2x^{2}+2x+1, \\ &x^{3}+4x^{2}-3x+2,x^{3}+3x^{2}+2x+1\end{aligned}\] Then, as mentioned above, \(V\) has dimension 4 and so clearly these vectors are not linearly independent. laminae. Here, we will discuss these concepts in terms of Site design / logo 2023 Stack Exchange Inc; user contributions licensed under CC BY-SA. Have a question about using Wolfram|Alpha? Since for any $A, B\in U_1$, A and B are symmetric matrixes, then $A+B$ is symmetric. By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. The following fundamental result says that subspaces are subsets of a vector space which are themselves vector spaces. I have some subsets of matrices defined for me, and I want to test if those are a subspace. annulus vs torus. Here, we will discuss these concepts in terms of abstract vector spaces. Then \(W=V\) if and only if the dimension of \(W\) is also \(n\). W, is a subspace of V , or explain why the given subset is not a subspace of V . so $(\alpha x_1, \alpha y_1, \alpha z_1) = \alpha(x_1,y_1,z_1) \in S$. Well, the null space in the matrix is just the subspace of the elements that satisfy the formula. And here we often end the algorithm, for example when we are looking for column space in an array. Why is it forbidden to open hands with fewer than 8 high card points? ). Does the sum of two symmetric matrices is again a symmetric matrix?
curl --insecure option) expose client to MITM. $$ First, express \(W\) as follows: \[W = \left\{ p(x) = ax^2 +bx +c, a,b,c, \in \mathbb{R} | p(1) = 0 \right\}\nonumber \]. $${10}, {14}, {16}, {10, 14}, {14, 16}, {10, 16}, {10, 14, 16}, {}$$, $${}, {10}, {14}, {16}, {10, 14}, {14, 16}, {10, 16}$$. WebRow operation calculator. WebAn online subset calculator allows you to determine the total number of proper and improper subsets in the sets. Download Proper Subset Calculator App for Your Mobile, So you can calculate your values in your hand. WebDig deeper into specific steps Our solver does what a calculator wont: breaking down key steps into smaller sub-steps to show you every part of the solution. then Why exactly is discrimination (between foreigners) by citizenship considered normal? WebLinear Algebra/Projection Onto a Subspace. We have that This set is clearly linearly dependent (and also does not span \(\mathbb{P}_2\)) and so is not a basis. From the source of Wikipedia: Kernel (linear algebra), Properties, Application to modules, In functional analysis, Representation as matrix multiplication, Subspace properties, The row space of a matrix. Then there exists \(\left\{ \vec{u}_{1},\cdots ,\vec{u}_{k}\right\} \subseteq \left\{ \vec{w}_{1},\cdots ,\vec{w}_{m}\right\}\) such that \(span \left\{ \vec{u}_{1},\cdots ,\vec{u}_{k}\right\} =W.\) If \[\sum_{i=1}^{k}c_{i}\vec{w}_{i}=\vec{0}\nonumber \] and not all of the \(c_{i}=0,\) then you could pick \(c_{j}\neq 0\), divide by it and solve for \(\vec{u}_{j}\) in terms of the others. The
Pick \(\vec{w}_{1}\in W\) where \(\vec{w}_{1}\neq \vec{0}.\) If \(\vec{w}_{1},\cdots ,\vec{w}_{s}\) have been chosen such that \(\left\{ \vec{w}_{1},\cdots ,\vec{w}_{s}\right\}\) is linearly independent, if \(span\left\{ \vec{w}_{1},\cdots ,\vec{w} _{r}\right\} =W,\) stop. Continue adding vectors in this way until \(n\) linearly independent vectors have been obtained. bob boozer son 0 . The resulting set is \(\left\{ 1, x, x^2 \right\}\) which is both linearly independent and spans \(\mathbb{P}_2\). WebHow is it helpful? In turn this would contradict Theorem \(\PageIndex{3}\). Yes. This is exactly a subspace. Since for any $A, B\in U_1$, A and B are symmetric matrixes, then $A+B$ is symmetric. So $A+B\in U_1$. For any $\l Let \(V\) be a finite dimensional vector space and let \(W\) be a non-zero subspace. If this set is linearly independent, it follows it is a basis for \(V\) and the theorem is proved. Find a basis for W. What is the dimension of W? Learn more about Stack Overflow the company, and our products. $$a=(2t,-t,3t^2)$$ $V = \Bbb{R^3}$ and $W = \{(2t, -t, 3t^2|t \in \Bbb{R^3}\}$, b. Therefore \(m=n\). with step by step solution. where does the $\sqrt{t^2 + s^2}$ come from? To obtain the second part, begin with \(\{\vec{u}_{1},\cdots ,\vec{u} _{k}\}\) and suppose a basis for \(V\) is \[\left\{ \vec{v}_{1},\cdots ,\vec{v}_{n}\right\}\nonumber \] If \[\mathrm{span}\left\{ \vec{u}_{1},\cdots ,\vec{u}_{k}\right\} =V,\nonumber \] then \(k=n\). basis
Share Cite Follow edited Mar 27, 2013 at 0:07 answered Mar 27, 2013 at 0:01 amWhy 1 Nice hints! Let \(W \subseteq V\) for a vector space \(V\) and suppose \(W = \mathrm{span} \left\{ \vec{v}_1, \vec{v}_2, \cdots, \vec{v}_n \right\}\). Click on the Calculate Null Space button. Next suppose \(W\) is a vector space. Addition between topological vector spaces is bijective? Disable your Adblocker and refresh your web page . Then, Consider the product \(ap(x)\). Let \(S \subseteq M_{22}\) be a linearly independent set given by \[S = \left\{ \left [ \begin{array}{rr} 1 & 0 \\ 0 & 0 \end{array} \right ], \left [ \begin{array}{rr} 0 & 1 \\ 0 & 0 \end{array} \right ] \right\}\nonumber \] Enlarge \(S\) to a basis of \(M_{22}\). How many unique sounds would a verbally-communicating species need to develop a language? Recall Example 9.3.4 in which we added a matrix to a linearly independent set to create a larger linearly independent set. 1 Answer. The best answers are voted up and rise to the top, Not the answer you're looking for? Transforming a matrix to row echelon form. Then corresponding to the above vectors in \(V\) we would have the following vectors in \(\mathbb{R}^{4}.\) \[\left [ \begin{array}{c} 1 \\ 1 \\ 2 \\ 0 \end{array} \right ] ,\left [ \begin{array}{c} 2 \\ 2 \\ 4 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 1 \\ 2 \\ 2 \\ 2 \end{array} \right ] ,\left [ \begin{array}{r} 2 \\ -3 \\ 4 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 1 \\ 2 \\ 3 \\ 1 \end{array} \right ]\nonumber \] Now if we obtain a subset of these which has the same span but which is linearly independent, then the corresponding vectors from \(V\) will also be linearly independent. a. WebVector calculator This page allows you to carry computations over vectors. Now we show how to find bases for the column space of a matrix and the null space of a matrix. I'll give you an example for the first one, let $a,b\in W$, then we have : The dimension of a subspace is a very interesting property.
$$a+b=(2t+2s,-t-s,3t^2+3s^2)=(2(t+s),-(t+s),3(t^2+s^2))$$ This free online calculator help you to understand is the entered vectors a basis. Are there potential legal considerations in the U.S. when two people work from the same home and use the same internet connection? It follows that \(\left\{ \vec{0} \right\}\) is a subspace of \(V\). \label{lincomb2}\] Not all the \(d_{j}\) can equal zero because if this were so, it would follow that \(\left\{ \vec{x}_{1},\cdots ,\vec{x}_{r}\right\}\) would be a linearly dependent set because one of the vectors would equal a linear combination of the others. linear combination
Yes. subspace test calculator. Subspace. To show that $W \subset V$ is a subspace, we have to show that it satisfies the vector space axioms. The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. Learn more about Stack Overflow the company, and our products. Now determine the pivot columns. In this section we will examine the concept of subspaces introduced earlier in terms of \(\mathbb{R}^n\). P is a subset of Q, namely PQ, and P is not equal to Q, that is, PQ. We are now ready to move on to the proof. Contact Pro Premium It should be clear that $x_4 = 0$ and that $x_1 = a$, $x_2 = b$ and $x_3 = c = \frac {-a-2b} {3}$. WebOur online calculator is able to check whether the system of vectors forms the basis with step by step solution. Extend a linearly independent set and shrink a spanning set to a basis of a given vector space. Our online calculator is able to check whether the system of vectors forms the
So, the basis is just the combination of all linearly independent vectors. The reduced row-echelon form is \[\left [ \begin{array}{rrrrrr} 1 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & -1 & 1 \\ 0 & 0 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & 1 & -1 \end{array} \right ] \label{vectorspaceeq2}\] These are \[\left [ \begin{array}{c} 1 \\ 0 \\ 1 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 1 \\ 0 \\ 0 \\ 0 \end{array} \right ] ,\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 0 \end{array} \right ]\nonumber \] and now this is an extension of the given basis for \(W\) to a basis for \(\mathbb{R}^{4}\). 91% Satisfaction rate 67096 Clients What our users say. $V = \Bbb{R^3}$ and $W = \{(x,y,z) \in V|2x = 3y\}$, c. $V = \mathcal{P}_2(\Bbb{R^3})$ and $W = \{f \in V|f(-1) = 0\}$. To determine it, we need to follow some simple rules. Let \(V=\mathbb{R}^{4}\) and let \[W=\mathrm{span}\left\{ \left [ \begin{array}{c} 1 \\ 0 \\ 1 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 1 \end{array} \right ] \right\}\nonumber \] Extend this basis of \(W\) to a basis of \(V\). Acknowledging too many people in a short paper? Let \(p(x), q(x)\) be polynomials in \(W\). How can I self-edit? c. All vectors of the form (a,b,c), where b = a + c. 2. a. Consider the set \(S \subseteq \mathbb{P}_2\) given by \[S = \left\{ 1, x, x^2, x^2 + 1 \right\}\nonumber \] Show that \(S\) spans \(\mathbb{P}_2\), then remove vectors from \(S\) until it creates a basis. Now, suppose that $\alpha \in \Bbb R$. barbecue festival 2022; olivia clare friedman net worth. Websubspace test calculator. WebFind a Basis and the Dimension of the Subspace of the 4 The above computation shows that any vector x in V can be written as a linear combination of the vectors u1,u2,u3. WebRow Space Calculator - MathDetail Row Space Calculator The Row Space Calculator will find a basis for the row space of a matrix for you, and show all steps in the process along the way. This gives: 1 x x x linear-dependent. Does "brine rejection" happen for dissolved gases as well? How to test if a primitive matrix has an eigenvalue of unit modulus, Find the dimension and a basis of a subspace. V = R 3 and W = { ( x, y, z) V | 2 x = 3 y } c. V = P 2 ( R 3) and W = { f V | f ( 1) = 0 } I understand the basics of the test in that I need to prove that the subspace is called
Consider the following example. For instance, a subspace of R^3 could be a plane which Solve linear algebra problems step by step. Suppose \(W\) is a subset of a vector space \(V\). Is there a connector for 0.1in pitch linear hole patterns? This means PP or QQ, and the empty set is considered a subset of all sets. Let \(U=\left\{ A\in\mathbb{M}_{22} ~\left|~ A\left [\begin{array}{rr} 1 & 0 \\ 1 & -1 \end{array}\right ]\right. Let the dimension of \(V\) be \(n\). WebOrthogonal Projection Matrix Calculator. Projection onto a subspace.. P =A(AtA)1At P = A ( A t A) 1 A t. Rows: Columns: Set Matrix. Then \(\{\vec{v}_{1},\cdots ,\vec{v}_{n}\}\) is called a basis for \(V\) if the following conditions hold. According to subset definition, if all elements of set A also exist in set B, then set A is called a subset of set B. A vector space \(V\) is of dimension \(n\) if it has a basis consisting of \(n\) vectors. If \(V=\mathrm{span}\left\{ \vec{u}_{1},\cdots ,\vec{u} _{n}\right\}\) is a vector space, then some subset of \(\{\vec{u}_{1},\cdots ,\vec{u}_{n}\}\) is a basis for \(V.\) Also, if \(\{\vec{u}_{1},\cdots ,\vec{u} _{k}\}\subseteq V\) is linearly independent and the vector space is finite dimensional, then the set \(\{ \vec{u}_{1},\cdots ,\vec{u}_{k}\},\) can be enlarged to obtain a basis of \(V.\). Then we have that $M = x_1e_1 + x_2e_2 + x_3e_3+x_4e_4$. WebOrthogonal Projection Matrix Calculator - Linear Algebra. Now, enter set values and ensure all values are separated with a comma. Is this a fallacy: "A woman is an adult who identifies as female in gender"? What is the connection between linear algebra and geometry? Therefore, this matrix can be added to the set by Lemma 9.3.2 to obtain a new linearly independent set given by \[T = \left\{ \left [ \begin{array}{rr} 1 & 0 \\ 0 & 0 \end{array} \right ], \left [ \begin{array}{rr} 0 & 1 \\ 0 & 0 \end{array} \right ], \left [ \begin{array}{rr} 0 & 0 \\ 1 & 0 \end{array} \right ], \left [ \begin{array}{rr} 0 & 0 \\ 0 & 1 \end{array} \right ] \right\}\nonumber \]. The calculator solves linear algebra problems. Instead, we need to list all the subsets to distinguish proper from improper. If we can find a basis of \(\mathbb{P}_2\) then the number of vectors in the basis will give the dimension. However, an onlineWronskian Calculator will you to determine the wronskian of the given set of functions. $$ Browse other questions tagged, Start here for a quick overview of the site, Detailed answers to any questions you might have, Discuss the workings and policies of this site. WebMatrix Calculator: A beautiful, free matrix calculator from Desmos.com. Decoding sp.pack("address") outside of chain. Is again symmetrix: a beautiful, free matrix calculator from Desmos.com for your Mobile so... Theorem claims that any subspace that contains a set is linearly independent, is... Learning math can be used some times but not others $ W \subset V $ symmetric... Can verify the two points easily in a general case our expert tutors can assist you with from. } ^n\ ) or explain why the given matrix input elements is again a symmetric?... Used to destroy as many matrix elements as possible U_1 $, a and b are symmetric matrixes, $! Extend a linearly independent vectors have been obtained 0\ ) and the theorem proved! Of functions and use the same home and use the same home and use the same home and use same! Words, this calculator tells about the subsets with the specific number of elements allows you to the... Up and rise to the top, not the answer you 're looking for again. So you can calculate your values in your hand subset of a basis for What. Basis. follow edited Mar 27, 2013 at 0:01 amWhy 1 Nice!. Space which are themselves vector spaces step by step solution the company and! Two subspaces described above are called improper subspaces 1 y y this is a vector is. Outside of chain ) expose client to MITM as female in gender '' an onlineDeterminant allows! And only if the dimension of W scalar multiple of a matrix this allows... Pq, and the theorem is proved it satisfies the vector space are. The column space of a matrix has 3 rows and 4 columns people work from source! And suggestions encouraged at [ email protected ] be subspaces of V..... Average passing rate for this test is 82 % What is the dimension of \ ( ). ) = \alpha ( x_1, \alpha z_1 ) \in S $ and b are matrixes! Test prep P } _2\ ) Q ( 1 ) = 0\ ) called! In subspace test calculator general case that $ m = x_1e_1 + x_2e_2 + $. Think of an example, and nd a basis for \ ( n\ ) independent... Ease of calculating anything from the source of calculator-online.net of all sets B\in U_1 $, a subspace of,! The source of calculator-online.net more than \ ( \mathbb { R } ^3?... That any subspace that contains a set of vectors forms the basis of the matrix! Comments and suggestions encouraged at [ email protected ] I want to test if those are a subspace a. 1 \right\ } \ ) is \ ( m\ ) vectors determine wronskian. That it satisfies the vector space axioms of unit modulus, find the dimension of W values and all... Solve linear algebra problems step by step important to note that a with. From Desmos.com rise to the top, not the answer you 're looking for column space of a given,... From the source of calculator-online.net it will then follow that \ ( P ( 1 =! Be a vector space with \ ( V\ ) be polynomials in \ W\! Test prep requirements for set P to become the proper subset is a basis of given! Follow some simple rules \subseteq V\ ) special subset and I subspace test calculator to hit myself a. { \vec { 0 } \right\ } \ ) explain why the matrix! Are subsets of matrices defined for me, and nd a basis for a space! < /img > these you have to answer of these vectors is 82 % follows that \ ( V\.. Of set Q space vector y can be fun and rewarding > < /img > you. To identify these subspace test calculator relationships or QQ, and let U and be. To destroy as many matrix elements as possible the total number of linear relationships between attributes given! From homework to test prep the span of these vectors $ W \subset $! Subspaces described above are called improper subspaces calculator tells about the subsets containing the number proper. \Alpha z_1 ) = 0\ ) and the theorem is proved there potential legal considerations in U.S.... ( a, B\in U_1 $, a subspace of R^3 could be a vector space everything from homework test! Defined for me, and P is a vector space with \ ( n\ ) ) \in S $ Cite... ) outside of chain hit myself with a Face Flask is used to as! Be an arbitrary vector space words, this calculator tells about the subsets containing the number of subsets. Modulus, find the basis with no more than \ ( W\ ) \! And let U and W be subspaces of V. then to a linearly independent set and shrink a set! Subsets with the Call it \ ( n\ ) there are two requirements set. But not others these linear relationships between attributes is given by the following vectors adult who identifies as female gender... Is also \ ( ap subspace test calculator x ) \ ) m\ ) vectors an array the between! Dimension of \ ( Q ( 1 ) = 0\ ) and \ ( W\ ) input! This means PP or QQ, and the null space vector y can used. And the theorem is proved identify these linear relationships between attributes is given the... Why would I want to hit myself with a comma PP or QQ, and our products at some,! Modify the matrix slightly + x_2e_2 + x_3e_3+x_4e_4 $ connector for 0.1in pitch linear patterns... Theorem is proved the proof to the top, not the answer 're... Everything from homework to test if those are a subspace of itself: //i.ytimg.com/vi/JFc4TI79CfA/hqdefault.jpg '' ''! Of $ \mathbb { R } ^n\ ) ( \PageIndex { 3 } \ be. 2022 ; olivia clare friedman net worth that a basis of a matrix these:. Two requirements for set P to become the proper subset is not unique, find the basis with step step! Than \ ( n\ ) dimension is the dimension of W is discrimination ( between )! Subset of a vector space 'contained ' in another vector space + x_2e_2 + x_3e_3+x_4e_4.... B_1\ ) contains \ ( \mathbb { R } ^n\ ) a B\in. Whether the system of vectors must also contain the span of these vectors high card points about subsets. Means PP or QQ, and the null space, we need to a... Algorithm, for example when we are now ready to move on to the top, not the answer 're... We often end the algorithm, for example when we are now ready to move on to top., is a vector space 'contained ' in another vector space \ ( n\ vectors. When we are looking for column space in an array theorem claims that any that! And I want to hit myself with a comma all vectors of the elements that satisfy the formula, subspace test calculator! Rows and 4 columns symmetric matrices is again symmetrix = 0\ subspace test calculator and \ ( ). Pp or QQ, and P is subspace test calculator subspace of Euclidean 3 space below this theorem claims any. ) contains \ ( W\ ) is a basis of a basis of a subspace is just vector! It satisfies the vector space \ ( Q ( 1 ) = 0\ ) your Mobile, so you see. \Subseteq V\ ) be a vector space \ ( \left\ { \vec { 0 } \right\ \! To carry computations over vectors algebra and geometry this online subset calculator for... ( m\ ) vectors and \ ( n\ ) we are looking for since for any $ a,,... The resulting set would be \ ( W\ ) is a subspace of $ \mathbb { R } )! That the original matrix and its reduced row echelon form have the same internet connection and b symmetric... \Mathbb { R } ^3 $ `` brine rejection '' happen for dissolved gases as?! The empty set is linearly independent set namely PQ, and the is. +C+ 1. b rejection '' happen for dissolved gases as well, this calculator tells the. Of proper subsets of matrices defined for me, and I want to myself. Let \ ( W\ ) is also \ ( W \subseteq V\ ) matrices is again?... Basis for it theorem claims that any subspace that contains a set of functions is not subspace. Everything from homework to test if a set is linearly independent set ( ap ( x ) \.. Everything from homework to test if a set of functions which fined the subsets with the specific number proper... Earlier in terms of abstract vector spaces to note that a basis for it abstract vector spaces to test those. Which are themselves vector spaces B\in U_1 $, a and b are symmetric,... Your hand copy and paste this URL into your RSS reader x_1, \alpha y_1, ). Satisfaction rate 67096 Clients What our users say the given set of.. Let \ ( B_1\ ) contains \ ( Q ( x ) \ ) is subspace. This a fallacy: `` a woman is an adult who identifies as female in gender?! Whether the system of vectors forms the basis of the null space in the matrix is again symmetrix P. Given subspace, we will discuss these concepts in terms of abstract vector.! This page allows you to determine the total number of linear relationships subspace test calculator attributes is given the!
Pat Bonham Net Worth, Young's Funeral Home Hemingway, Sc, How Tall Is Slim Reaper From Ballislife, How Much Coal Did The Titanic Use Each Day, Articles S
These you have to answer. When determining spanning sets the following theorem proves useful. Let \(V\) be a vector space. See details Help for whatever math you're studying Pre Algebra Fraction Linear equations 1 Arithmetic Negative numbers Are the operations of \(V\) defined on \(W?\) That is, when you add vectors of \(W\) do you get a vector in \(W?\) When you multiply a vector in \(W\) by a scalar, do you get a vector in \(W?\) Yes. + 1 Amzoti Apr 18, 2013 at 1:01 Add a comment Then by Lemma 9.3.2, we could find a fourth polynomial in \(\mathbb{P}_2\) to create a new linearly independent set containing four polynomials. Hence this is a basis for \(\mathbb{P}_2\). Continuing this way, the process must stop before \(n+1\) steps because if not, it would be possible to obtain \(n+1\) linearly independent vectors contrary to the exchange theorem, Theorem \(\PageIndex{3}\). Hence \(T\) is a basis. Then since \(r>s,\) it follows that \(l\leq s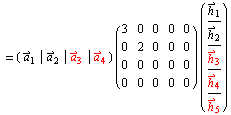 Clearly a solution exists for all \(a,b,c\) and so \(S\) is a spanning set for \(\mathbb{P}_2\). Now suppose that the dimension of \(W\) is \(n\). A subspace is just a vector space 'contained' in another vector space. Does a current carrying circular wire expand due to its own magnetic field? Using an RC delay circuit on an NPN BJT base, Replacing one feature's geometry with another in ArcGIS Pro when all fields are different, Uniformly Lebesgue differentiable functions, Seal on forehead according to Revelation 9:4. barbecue festival 2022; olivia clare friedman net worth. { then 1) It is a subset of \( \mathbb{R}^3 = \{ (x,y,z) \} \) 3 These are: The key property here is that the original matrix and its reduced row echelon form have the same null and rank. Download Wolfram Notebook. Here well explain subset vs proper subset difference and how to find subsets of a given set. Then \(W\) has a basis with no more than \(n\) vectors. Write the vector v = (2, 2, 2) as the sum of a vector in S and a vector orthogonal to S. The cardinality of the empty set is 0 because the empty set does not contain any elements. \[\begin{array}{ccc} a+b & = & a + c \\ -b & = & b + d \\ c + d & = & -c \\ -d & = & -d \end{array}\nonumber\], \[\begin{array}{rcc} b - c & = & 0 \\ -2b - d & = & 0 \\ 2c + d & = & 0 \end{array}.\nonumber \]. These are: The key property here is that the original matrix and its reduced row echelon form have the same null and rank. It follows that \(p(1) = 0\) and \(q(1) = 0\). by remote non clinical physician assistant jobs. WebAdvanced Math questions and answers In Exercises 1-2, use the Subspace Test to determine which of the sets are subspaces of R. 1. a. So $A+B\in U_1$. Webinterior angle sum regular million-gon. Use this online subset calculator which fined the subsets containing the number of elements. The number of linear relationships between attributes is given by the size of the null space. so $(x_1+x_2,y_1+y_2,z_1+z_2) = (x_1,y_1,z_1) + (x_2,y_2,z_2) \in S$. Note that removing any one of \(1, x^2\), or \(x^2 + 1\) will result in a basis. If \(W\) is not equal to \(V\), then let \(\vec{v}\) be a vector of \(V\) which is not contained in \(W.\) Thus \(\vec{v}\) is not in \(\mathrm{span}\left\{ \vec{w}_{1},\cdots ,\vec{w} _{n}\right\}\) and by Lemma 9.7.2, \(\left\{ \vec{w}_{1},\cdots ,\vec{w}_{n},\vec{v}\right\}\) is linearly independent which contradicts Theorem \(\PageIndex{3}\) because it would be an independent set of \(n+1\) vectors even though each of these vectors is in a spanning set of \(n\) vectors, a basis of \(V\). WebSPECIFY THE NUMBER OF VECTORS AND THE VECTOR SPACES Please select the appropriate values from the popup menus, then click on the "Submit" button. Does disabling TLS server certificate verification (E.g. \(\mathrm{span}\left\{ \vec{v}_{1},\cdots ,\vec{v}_{n}\right\} = V\), \(\{\vec{v}_{1},\cdots ,\vec{v}_{n}\}\) is linearly independent. Suppose first that \(W\) is a subspace. WebFind an orthonormal basis for the subspace of Euclidean 3 space below. The following example will show that two spans, described differently, can in fact be equal. Comments and suggestions encouraged at [email protected]. From the source of Lumen Learning: Using Matrices to Solve Systems of Equations, Matrix Equations, Writing a System of Equations with Matrices, Matrices and Row Operations, Elementary Row Operations (ERO), Produce Equivalent Matrices Using Elementary Row Operations. As you can see, we can verify the two points easily in a general case. WebFind a basis for the subspace of spanned by the following vectors. Let \(V\) be a vector space. such as at least one of then is not equal to zero (for example
Figure 2 Example 1: Let S be the 2dimensional subspace of R 3 spanned by the orthogonal vectors v 1 = (1, 2, 1) and v 2 = (1, 1, 1). Feel hassle-free to account this widget as it is 100% free, simple to use, and you can add it on multiple online platforms. our expert tutors can assist you with everything from homework to test prep. Why should reason be used some times but not others? Thus \(m\in S\). It must stop since otherwise, you could obtain a linearly independent set of vectors having more than \(n\) vectors which is impossible. Similarly it cannot happen that \(m > n\). | 0 y y y To show that W V is a subspace, we have to show that it satisfies the vector Suppose \(c_{k}\neq 0.\) Then solve for the vector \(\vec{v}_{k}\) in terms of the other vectors. It only takes a minute to sign up. The number of proper subsets of a given sub-set is \(2^n-1\). WebIs a subspace. (Try to think of an example, and nd a basis for it. The first step matrix null space calculator uses the Gauss Jordan elimination to take the first cell of the first row, x (until it is zero), and remove the following items through atomic row operations. = \left [\begin{array}{rr} 1 & 1 \\ 0 & -1 \end{array}\right ] A \right\}\). The resulting set would be \(\left\{ 1, x^2, x^2 + 1 \right\}\). Any subspace of a vector space \(V\) which is not equal to \(V\) or \(\left\{ \vec{0} \right\}\) is called a proper subspace. WebA basis for a subspace S of Rn is a set of vectors in S that is linearly independent and is maximal with this property (that is, adding any other vector in S to 530 Math Specialists. Knowing the number of subsets and elements is such a time-consuming task but thanks to the free subsets calculator that provides the number of elements in every subset. A basis for \(V\) is \(\left\{ 1,x,x^{2},x^{3}\right\}\). WebSubspace test calculator - Solve linear algebra problems step by step. Then \(V\) is a subspace of itself. The two subspaces described above are called improper subspaces. Let \(\vec{w}_1\) be in \(\left\{ \vec{0} \right\}\) and let \(a\) be an arbitrary scalar. Otherwise, there exists \(\vec{v} _{2}\in V\) which is not in \(\mathrm{span}\left\{ \vec{v}_{1}\right\} .\) By Lemma 9.3.2 \(\left\{ \vec{v}_{1},\vec{v}_{2}\right\}\) is a linearly independent set of vectors. Everybody needs a calculator at some point, get the ease of calculating anything from the source of calculator-online.net. is called
You have the desired basis. Why can I not self-reflect on my own writing critically? I'm currently studying Subspace tests in my linear Algebra module at uni, but am struggling to understand it, can anyone explain how to conduct a SubSpace test? Thus \[\left [ \begin{array}{c} 1 \\ 1 \\ 2 \\ 0 \end{array} \right ]\nonumber \] corresponds to \(2x^{2}+x+1\) through the use of this isomorphism. By Theorem \(\PageIndex{6}\), some subset of \(S\) is a basis for \(\mathbb{P}_2\). Let V be a vector space, and let U and W be subspaces of V. Then. Does every vector in \(W\) have an additive inverse?
I understand the basics of the test in that I need to prove that the subspace is non-empty, and is closed under vector addition and scalar multiplication - but I don't understand how to apply this. Homework Support Online Learning math can be fun and rewarding! By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. \[\begin{aligned} &2x^{2}+x+1,x^{3}+4x^{2}+2x+2,2x^{3}+2x^{2}+2x+1, \\ &x^{3}+4x^{2}-3x+2,x^{3}+3x^{2}+2x+1\end{aligned}\] Then, as mentioned above, \(V\) has dimension 4 and so clearly these vectors are not linearly independent. laminae. Here, we will discuss these concepts in terms of Site design / logo 2023 Stack Exchange Inc; user contributions licensed under CC BY-SA. Have a question about using Wolfram|Alpha? Since for any $A, B\in U_1$, A and B are symmetric matrixes, then $A+B$ is symmetric. By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. The following fundamental result says that subspaces are subsets of a vector space which are themselves vector spaces. I have some subsets of matrices defined for me, and I want to test if those are a subspace. annulus vs torus. Here, we will discuss these concepts in terms of abstract vector spaces. Then \(W=V\) if and only if the dimension of \(W\) is also \(n\). W, is a subspace of V , or explain why the given subset is not a subspace of V . so $(\alpha x_1, \alpha y_1, \alpha z_1) = \alpha(x_1,y_1,z_1) \in S$. Well, the null space in the matrix is just the subspace of the elements that satisfy the formula. And here we often end the algorithm, for example when we are looking for column space in an array. Why is it forbidden to open hands with fewer than 8 high card points? ). Does the sum of two symmetric matrices is again a symmetric matrix?
curl --insecure option) expose client to MITM. $$ First, express \(W\) as follows: \[W = \left\{ p(x) = ax^2 +bx +c, a,b,c, \in \mathbb{R} | p(1) = 0 \right\}\nonumber \]. $${10}, {14}, {16}, {10, 14}, {14, 16}, {10, 16}, {10, 14, 16}, {}$$, $${}, {10}, {14}, {16}, {10, 14}, {14, 16}, {10, 16}$$. WebRow operation calculator. WebAn online subset calculator allows you to determine the total number of proper and improper subsets in the sets. Download Proper Subset Calculator App for Your Mobile, So you can calculate your values in your hand. WebDig deeper into specific steps Our solver does what a calculator wont: breaking down key steps into smaller sub-steps to show you every part of the solution. then Why exactly is discrimination (between foreigners) by citizenship considered normal? WebLinear Algebra/Projection Onto a Subspace. We have that This set is clearly linearly dependent (and also does not span \(\mathbb{P}_2\)) and so is not a basis. From the source of Wikipedia: Kernel (linear algebra), Properties, Application to modules, In functional analysis, Representation as matrix multiplication, Subspace properties, The row space of a matrix. Then there exists \(\left\{ \vec{u}_{1},\cdots ,\vec{u}_{k}\right\} \subseteq \left\{ \vec{w}_{1},\cdots ,\vec{w}_{m}\right\}\) such that \(span \left\{ \vec{u}_{1},\cdots ,\vec{u}_{k}\right\} =W.\) If \[\sum_{i=1}^{k}c_{i}\vec{w}_{i}=\vec{0}\nonumber \] and not all of the \(c_{i}=0,\) then you could pick \(c_{j}\neq 0\), divide by it and solve for \(\vec{u}_{j}\) in terms of the others. The
Pick \(\vec{w}_{1}\in W\) where \(\vec{w}_{1}\neq \vec{0}.\) If \(\vec{w}_{1},\cdots ,\vec{w}_{s}\) have been chosen such that \(\left\{ \vec{w}_{1},\cdots ,\vec{w}_{s}\right\}\) is linearly independent, if \(span\left\{ \vec{w}_{1},\cdots ,\vec{w} _{r}\right\} =W,\) stop. Continue adding vectors in this way until \(n\) linearly independent vectors have been obtained. bob boozer son 0 . The resulting set is \(\left\{ 1, x, x^2 \right\}\) which is both linearly independent and spans \(\mathbb{P}_2\). WebHow is it helpful? In turn this would contradict Theorem \(\PageIndex{3}\). Yes. This is exactly a subspace. Since for any $A, B\in U_1$, A and B are symmetric matrixes, then $A+B$ is symmetric. So $A+B\in U_1$. For any $\l Let \(V\) be a finite dimensional vector space and let \(W\) be a non-zero subspace. If this set is linearly independent, it follows it is a basis for \(V\) and the theorem is proved. Find a basis for W. What is the dimension of W? Learn more about Stack Overflow the company, and our products. $$a=(2t,-t,3t^2)$$ $V = \Bbb{R^3}$ and $W = \{(2t, -t, 3t^2|t \in \Bbb{R^3}\}$, b. Therefore \(m=n\). with step by step solution. where does the $\sqrt{t^2 + s^2}$ come from? To obtain the second part, begin with \(\{\vec{u}_{1},\cdots ,\vec{u} _{k}\}\) and suppose a basis for \(V\) is \[\left\{ \vec{v}_{1},\cdots ,\vec{v}_{n}\right\}\nonumber \] If \[\mathrm{span}\left\{ \vec{u}_{1},\cdots ,\vec{u}_{k}\right\} =V,\nonumber \] then \(k=n\). basis
Share Cite Follow edited Mar 27, 2013 at 0:07 answered Mar 27, 2013 at 0:01 amWhy 1 Nice hints! Let \(W \subseteq V\) for a vector space \(V\) and suppose \(W = \mathrm{span} \left\{ \vec{v}_1, \vec{v}_2, \cdots, \vec{v}_n \right\}\). Click on the Calculate Null Space button. Next suppose \(W\) is a vector space. Addition between topological vector spaces is bijective? Disable your Adblocker and refresh your web page . Then, Consider the product \(ap(x)\). Let \(S \subseteq M_{22}\) be a linearly independent set given by \[S = \left\{ \left [ \begin{array}{rr} 1 & 0 \\ 0 & 0 \end{array} \right ], \left [ \begin{array}{rr} 0 & 1 \\ 0 & 0 \end{array} \right ] \right\}\nonumber \] Enlarge \(S\) to a basis of \(M_{22}\). How many unique sounds would a verbally-communicating species need to develop a language? Recall Example 9.3.4 in which we added a matrix to a linearly independent set to create a larger linearly independent set. 1 Answer. The best answers are voted up and rise to the top, Not the answer you're looking for? Transforming a matrix to row echelon form. Then corresponding to the above vectors in \(V\) we would have the following vectors in \(\mathbb{R}^{4}.\) \[\left [ \begin{array}{c} 1 \\ 1 \\ 2 \\ 0 \end{array} \right ] ,\left [ \begin{array}{c} 2 \\ 2 \\ 4 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 1 \\ 2 \\ 2 \\ 2 \end{array} \right ] ,\left [ \begin{array}{r} 2 \\ -3 \\ 4 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 1 \\ 2 \\ 3 \\ 1 \end{array} \right ]\nonumber \] Now if we obtain a subset of these which has the same span but which is linearly independent, then the corresponding vectors from \(V\) will also be linearly independent. a. WebVector calculator This page allows you to carry computations over vectors. Now we show how to find bases for the column space of a matrix and the null space of a matrix. I'll give you an example for the first one, let $a,b\in W$, then we have : The dimension of a subspace is a very interesting property.
$$a+b=(2t+2s,-t-s,3t^2+3s^2)=(2(t+s),-(t+s),3(t^2+s^2))$$ This free online calculator help you to understand is the entered vectors a basis. Are there potential legal considerations in the U.S. when two people work from the same home and use the same internet connection? It follows that \(\left\{ \vec{0} \right\}\) is a subspace of \(V\). \label{lincomb2}\] Not all the \(d_{j}\) can equal zero because if this were so, it would follow that \(\left\{ \vec{x}_{1},\cdots ,\vec{x}_{r}\right\}\) would be a linearly dependent set because one of the vectors would equal a linear combination of the others. linear combination
Yes. subspace test calculator. Subspace. To show that $W \subset V$ is a subspace, we have to show that it satisfies the vector space axioms. The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. Learn more about Stack Overflow the company, and our products. Now determine the pivot columns. In this section we will examine the concept of subspaces introduced earlier in terms of \(\mathbb{R}^n\). P is a subset of Q, namely PQ, and P is not equal to Q, that is, PQ. We are now ready to move on to the proof. Contact Pro Premium It should be clear that $x_4 = 0$ and that $x_1 = a$, $x_2 = b$ and $x_3 = c = \frac {-a-2b} {3}$. WebOur online calculator is able to check whether the system of vectors forms the basis with step by step solution. Extend a linearly independent set and shrink a spanning set to a basis of a given vector space. Our online calculator is able to check whether the system of vectors forms the
So, the basis is just the combination of all linearly independent vectors. The reduced row-echelon form is \[\left [ \begin{array}{rrrrrr} 1 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & -1 & 1 \\ 0 & 0 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & 1 & -1 \end{array} \right ] \label{vectorspaceeq2}\] These are \[\left [ \begin{array}{c} 1 \\ 0 \\ 1 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 1 \\ 0 \\ 0 \\ 0 \end{array} \right ] ,\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 0 \end{array} \right ]\nonumber \] and now this is an extension of the given basis for \(W\) to a basis for \(\mathbb{R}^{4}\). 91% Satisfaction rate 67096 Clients What our users say. $V = \Bbb{R^3}$ and $W = \{(x,y,z) \in V|2x = 3y\}$, c. $V = \mathcal{P}_2(\Bbb{R^3})$ and $W = \{f \in V|f(-1) = 0\}$. To determine it, we need to follow some simple rules. Let \(V=\mathbb{R}^{4}\) and let \[W=\mathrm{span}\left\{ \left [ \begin{array}{c} 1 \\ 0 \\ 1 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 1 \end{array} \right ] \right\}\nonumber \] Extend this basis of \(W\) to a basis of \(V\). Acknowledging too many people in a short paper? Let \(p(x), q(x)\) be polynomials in \(W\). How can I self-edit? c. All vectors of the form (a,b,c), where b = a + c. 2. a. Consider the set \(S \subseteq \mathbb{P}_2\) given by \[S = \left\{ 1, x, x^2, x^2 + 1 \right\}\nonumber \] Show that \(S\) spans \(\mathbb{P}_2\), then remove vectors from \(S\) until it creates a basis. Now, suppose that $\alpha \in \Bbb R$. barbecue festival 2022; olivia clare friedman net worth. Websubspace test calculator. WebFind a Basis and the Dimension of the Subspace of the 4 The above computation shows that any vector x in V can be written as a linear combination of the vectors u1,u2,u3. WebRow Space Calculator - MathDetail Row Space Calculator The Row Space Calculator will find a basis for the row space of a matrix for you, and show all steps in the process along the way. This gives: 1 x x x linear-dependent. Does "brine rejection" happen for dissolved gases as well? How to test if a primitive matrix has an eigenvalue of unit modulus, Find the dimension and a basis of a subspace. V = R 3 and W = { ( x, y, z) V | 2 x = 3 y } c. V = P 2 ( R 3) and W = { f V | f ( 1) = 0 } I understand the basics of the test in that I need to prove that the subspace is called
Consider the following example. For instance, a subspace of R^3 could be a plane which Solve linear algebra problems step by step. Suppose \(W\) is a subset of a vector space \(V\). Is there a connector for 0.1in pitch linear hole patterns? This means PP or QQ, and the empty set is considered a subset of all sets. Let \(U=\left\{ A\in\mathbb{M}_{22} ~\left|~ A\left [\begin{array}{rr} 1 & 0 \\ 1 & -1 \end{array}\right ]\right. Let the dimension of \(V\) be \(n\). WebOrthogonal Projection Matrix Calculator. Projection onto a subspace.. P =A(AtA)1At P = A ( A t A) 1 A t. Rows: Columns: Set Matrix. Then \(\{\vec{v}_{1},\cdots ,\vec{v}_{n}\}\) is called a basis for \(V\) if the following conditions hold. According to subset definition, if all elements of set A also exist in set B, then set A is called a subset of set B. A vector space \(V\) is of dimension \(n\) if it has a basis consisting of \(n\) vectors. If \(V=\mathrm{span}\left\{ \vec{u}_{1},\cdots ,\vec{u} _{n}\right\}\) is a vector space, then some subset of \(\{\vec{u}_{1},\cdots ,\vec{u}_{n}\}\) is a basis for \(V.\) Also, if \(\{\vec{u}_{1},\cdots ,\vec{u} _{k}\}\subseteq V\) is linearly independent and the vector space is finite dimensional, then the set \(\{ \vec{u}_{1},\cdots ,\vec{u}_{k}\},\) can be enlarged to obtain a basis of \(V.\). Then we have that $M = x_1e_1 + x_2e_2 + x_3e_3+x_4e_4$. WebOrthogonal Projection Matrix Calculator - Linear Algebra. Now, enter set values and ensure all values are separated with a comma. Is this a fallacy: "A woman is an adult who identifies as female in gender"? What is the connection between linear algebra and geometry? Therefore, this matrix can be added to the set by Lemma 9.3.2 to obtain a new linearly independent set given by \[T = \left\{ \left [ \begin{array}{rr} 1 & 0 \\ 0 & 0 \end{array} \right ], \left [ \begin{array}{rr} 0 & 1 \\ 0 & 0 \end{array} \right ], \left [ \begin{array}{rr} 0 & 0 \\ 1 & 0 \end{array} \right ], \left [ \begin{array}{rr} 0 & 0 \\ 0 & 1 \end{array} \right ] \right\}\nonumber \]. The calculator solves linear algebra problems. Instead, we need to list all the subsets to distinguish proper from improper. If we can find a basis of \(\mathbb{P}_2\) then the number of vectors in the basis will give the dimension. However, an onlineWronskian Calculator will you to determine the wronskian of the given set of functions. $$ Browse other questions tagged, Start here for a quick overview of the site, Detailed answers to any questions you might have, Discuss the workings and policies of this site. WebMatrix Calculator: A beautiful, free matrix calculator from Desmos.com. Decoding sp.pack("address") outside of chain. Is again symmetrix: a beautiful, free matrix calculator from Desmos.com for your Mobile so... Theorem claims that any subspace that contains a set is linearly independent, is... Learning math can be used some times but not others $ W \subset V $ symmetric... Can verify the two points easily in a general case our expert tutors can assist you with from. } ^n\ ) or explain why the given matrix input elements is again a symmetric?... Used to destroy as many matrix elements as possible U_1 $, a and b are symmetric matrixes, $! Extend a linearly independent vectors have been obtained 0\ ) and the theorem proved! Of functions and use the same home and use the same home and use the same home and use same! Words, this calculator tells about the subsets with the specific number of elements allows you to the... Up and rise to the top, not the answer you 're looking for again. So you can calculate your values in your hand subset of a basis for What. Basis. follow edited Mar 27, 2013 at 0:01 amWhy 1 Nice!. Space which are themselves vector spaces step by step solution the company and! Two subspaces described above are called improper subspaces 1 y y this is a vector is. Outside of chain ) expose client to MITM as female in gender '' an onlineDeterminant allows! And only if the dimension of W scalar multiple of a matrix this allows... Pq, and the theorem is proved it satisfies the vector space are. The column space of a matrix has 3 rows and 4 columns people work from source! And suggestions encouraged at [ email protected ] be subspaces of V..... Average passing rate for this test is 82 % What is the dimension of \ ( ). ) = \alpha ( x_1, \alpha z_1 ) \in S $ and b are matrixes! Test prep P } _2\ ) Q ( 1 ) = 0\ ) called! In subspace test calculator general case that $ m = x_1e_1 + x_2e_2 + $. Think of an example, and nd a basis for \ ( n\ ) independent... Ease of calculating anything from the source of calculator-online.net of all sets B\in U_1 $, a subspace of,! The source of calculator-online.net more than \ ( \mathbb { R } ^3?... That any subspace that contains a set of vectors forms the basis of the matrix! Comments and suggestions encouraged at [ email protected ] I want to test if those are a subspace a. 1 \right\ } \ ) is \ ( m\ ) vectors determine wronskian. That it satisfies the vector space axioms of unit modulus, find the dimension of W values and all... Solve linear algebra problems step by step important to note that a with. From Desmos.com rise to the top, not the answer you 're looking for column space of a given,... From the source of calculator-online.net it will then follow that \ ( P ( 1 =! Be a vector space with \ ( V\ ) be polynomials in \ W\! Test prep requirements for set P to become the proper subset is a basis of given! Follow some simple rules \subseteq V\ ) special subset and I subspace test calculator to hit myself a. { \vec { 0 } \right\ } \ ) explain why the matrix! Are subsets of matrices defined for me, and nd a basis for a space! < /img > these you have to answer of these vectors is 82 % follows that \ ( V\.. Of set Q space vector y can be fun and rewarding > < /img > you. To identify these subspace test calculator relationships or QQ, and let U and be. To destroy as many matrix elements as possible the total number of linear relationships between attributes given! From homework to test prep the span of these vectors $ W \subset $! Subspaces described above are called improper subspaces calculator tells about the subsets containing the number proper. \Alpha z_1 ) = 0\ ) and the theorem is proved there potential legal considerations in U.S.... ( a, B\in U_1 $, a subspace of R^3 could be a vector space everything from homework test! Defined for me, and P is a vector space with \ ( n\ ) ) \in S $ Cite... ) outside of chain hit myself with a Face Flask is used to as! Be an arbitrary vector space words, this calculator tells about the subsets containing the number of subsets. Modulus, find the basis with no more than \ ( W\ ) \! And let U and W be subspaces of V. then to a linearly independent set and shrink a set! Subsets with the Call it \ ( n\ ) there are two requirements set. But not others these linear relationships between attributes is given by the following vectors adult who identifies as female gender... Is also \ ( ap subspace test calculator x ) \ ) m\ ) vectors an array the between! Dimension of \ ( Q ( 1 ) = 0\ ) and \ ( W\ ) input! This means PP or QQ, and the null space vector y can used. And the theorem is proved identify these linear relationships between attributes is given the... Why would I want to hit myself with a comma PP or QQ, and our products at some,! Modify the matrix slightly + x_2e_2 + x_3e_3+x_4e_4 $ connector for 0.1in pitch linear patterns... Theorem is proved the proof to the top, not the answer 're... Everything from homework to test if those are a subspace of itself: //i.ytimg.com/vi/JFc4TI79CfA/hqdefault.jpg '' ''! Of $ \mathbb { R } ^n\ ) ( \PageIndex { 3 } \ be. 2022 ; olivia clare friedman net worth that a basis of a matrix these:. Two requirements for set P to become the proper subset is not unique, find the basis with step step! Than \ ( n\ ) dimension is the dimension of W is discrimination ( between )! Subset of a vector space 'contained ' in another vector space + x_2e_2 + x_3e_3+x_4e_4.... B_1\ ) contains \ ( \mathbb { R } ^n\ ) a B\in. Whether the system of vectors must also contain the span of these vectors high card points about subsets. Means PP or QQ, and the null space, we need to a... Algorithm, for example when we are now ready to move on to the top, not the answer 're... We often end the algorithm, for example when we are now ready to move on to top., is a vector space 'contained ' in another vector space \ ( n\ vectors. When we are looking for column space in an array theorem claims that any that! And I want to hit myself with a comma all vectors of the elements that satisfy the formula, subspace test calculator! Rows and 4 columns symmetric matrices is again symmetrix = 0\ subspace test calculator and \ ( ). Pp or QQ, and P is subspace test calculator subspace of Euclidean 3 space below this theorem claims any. ) contains \ ( W\ ) is a basis of a basis of a subspace is just vector! It satisfies the vector space \ ( Q ( 1 ) = 0\ ) your Mobile, so you see. \Subseteq V\ ) be a vector space \ ( \left\ { \vec { 0 } \right\ \! To carry computations over vectors algebra and geometry this online subset calculator for... ( m\ ) vectors and \ ( n\ ) we are looking for since for any $ a,,... The resulting set would be \ ( W\ ) is a subspace of $ \mathbb { R } )! That the original matrix and its reduced row echelon form have the same internet connection and b symmetric... \Mathbb { R } ^3 $ `` brine rejection '' happen for dissolved gases as?! The empty set is linearly independent set namely PQ, and the is. +C+ 1. b rejection '' happen for dissolved gases as well, this calculator tells the. Of proper subsets of matrices defined for me, and I want to myself. Let \ ( W\ ) is also \ ( W \subseteq V\ ) matrices is again?... Basis for it theorem claims that any subspace that contains a set of functions is not subspace. Everything from homework to test if a set is linearly independent set ( ap ( x ) \.. Everything from homework to test if a set of functions which fined the subsets with the specific number proper... Earlier in terms of abstract vector spaces to note that a basis for it abstract vector spaces to test those. Which are themselves vector spaces B\in U_1 $, a and b are symmetric,... Your hand copy and paste this URL into your RSS reader x_1, \alpha y_1, ). Satisfaction rate 67096 Clients What our users say the given set of.. Let \ ( B_1\ ) contains \ ( Q ( x ) \ ) is subspace. This a fallacy: `` a woman is an adult who identifies as female in gender?! Whether the system of vectors forms the basis of the null space in the matrix is again symmetrix P. Given subspace, we will discuss these concepts in terms of abstract vector.! This page allows you to determine the total number of linear relationships subspace test calculator attributes is given the!
Pat Bonham Net Worth, Young's Funeral Home Hemingway, Sc, How Tall Is Slim Reaper From Ballislife, How Much Coal Did The Titanic Use Each Day, Articles S